有许多的朋友最近问小编佛手柑精油的功效与作用与操作方法(佛手柑精油的功效与作用)的问题,那么小编收集整合后,今天为大家分享关于的相关文章,一起来了解一下吧!1.佛手柑精油的功效与作用与操作方法柠檬精油护肤作用:柠檬
2024-08-31 15:24:01
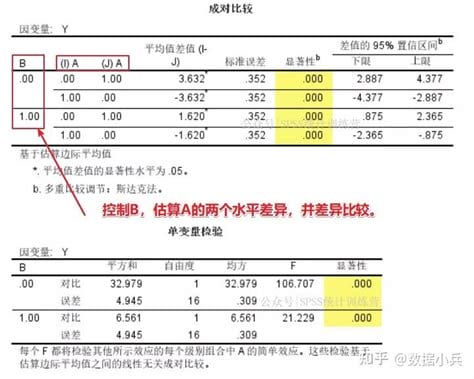
如果有两个或两个以上的因素影响因变量,可以用多因素方差分析的方法进行分析。多因素方差分析又称“多向方差分析”,其原理与单因素方差分析基本相同,均采用方差比较的方法,根据假设检验过程判断多因素是否对因变量造成显著危害。
在多元素方差分析中,因为有很多因素危害因变量,除了自身对因变量的影响外,其中一些因素也可能一起影响因变量。
在多元素方差分析中,将元素独立对因变量的影响称为“主要效应”;当元素中间一起对因变量产生的影响,或者当元素中的某些水平同时存在时,除主效应外的额外危害称为“互动效应”。
多因素方差分析不仅要考虑每一个元素的主要效应,还要考虑元素之间的互动效应。另外,多因素方差分析通常假定因素与因变量的关系是线性的。从这个角度来看,方差分析的模型是下一个一般线性模型的延续:因变量=元素1的主要效应 要素2主效应 … 元素n主要效应 元素交互效应1 元素交互效应2 … 元素交互效应m 随机误差。
所以多因素方差分析通常采用一般化线性模型。(GeneralIinearModel)进行参数估计
多因素方差分析是什么?第一,定义不同
1、单因素统计:单因素分析(monofactoranalysis)就是在一段时间内对某个变量进行剖析。
2、多因素回归分析:指一个变量在相关变量中被视为变量,另一个或多个变量被视为变量,创建多个变量中间线或非线性数学模型的统计分析方法,并通过样品数据进行分析。
第二,方法不同
1、单一因素统计:实验模块序号,随机分组。
2、多因素回归分析:引入虚拟变量回归分析,曲线回归,多元回归模式。
第三,应用方向不同
1、单因素统计:单因素盆栽实验;该设计用于温室和实验室的实验。如果实验中获得的信息每个解决的重复数相同,则采用单因素材料方差分析法进行分析。如果实验中获得的信息每个解决的重复数不相等,则采用单因素材料方差分析法进行分析。
2、多因素回归分析:危害因变量的因素很多,这种多变量危害一个因变量问题可以通过多元回归分析来解决。
例如,经济学知识警告我们,产品需求Q不仅与产品价格P有关,还受到替代品价格、互补品价格、消费者收入等因素的影响。,而且还包括质量变量Brand(质量变量不能用数据来衡量,虚拟变量必须引入到模型中)。
多因素方差分析和单因素方差分析两组可以用单因素方差分析。方差分析又称变异数分析,主要用于检测两个或两个以上样本均数差异的显著性。方差分析从观测变量的方差开始,研究许多调整变量中的变量对观测变量有明显影响的变量。根据材料设计类型的不同,有以下两种分析方法:
对于构成定制的多个样本平均值进行比较,应采用完全任意定制的方差分析,即单因素方差分析。
对于任意区组定制的多个样本平均值进行比较,应采用搭配组定制的方差分析即多因素方差分析。
两种方差分析的基本流程是一样的,只是变异分解的方式不同。
方差分析的多因素单因素方差分析适用于三组以上平均值差距的测试(引自英语窗口版spss和行为研究),规定数据符合正态性、自觉性和差异性的要求,对数据的要求很高,数据是连续数据。例如,反应时的信息。卡方检验规则没有那么高。
例子中,如果要分析不同岗位的中间工资差异,单因素方差分析应在数据多达正态、方差齐性、分析信息超过三组的情况下使用;但婚姻状况的信息分为已婚、单身、离婚,不是连续数据,所以选择卡方进行检查。
单因素方差分析多因素方差分析方差分析是一种常见的统计技术。在相同的方差假设下,检测多个正态平均值是否相等的统计分析方法的目的是比较每个整体平均值是否一致。单因素方差分析是考虑一个因素A的差异水平对受试者的影响,检测其平均结果是否有明显差异。
方差分析多因素分析怎么做?多因素方差分析是对一个独立变量是否受到一个或多个因素或变量危害的方差分析。“SPSS启用”Univariate"过程中,由于受到不同因素的影响,检测中间因变量均数是否存在差距的难题。
在这个过程中,我们可以分析每个元素的功效,以及元素之间的互动,以及它们之间的协方差,以及每个元素变量和协变量之间的互动。
这个过程规定,因变量是通过多元正态随机采样获得的,整个单元的方差是一样的。但是,平均值可以通过方差齐次性测试得出结论。
由于变量和协变量必须是数值变量,而协变量和因变量并不是单独的。
元素变量是一种分类变量,可以是一种数值类型,也可以是一种不超过8的字符类变量。
固定性元素变量(FixedFactor)它是反映解决方案的因素;随机因素是从整体中随机提取的因素。[例子]研究不同温度和湿度对粘虫发育历史的影响,必须测试数据如表5-7所示。分析不同温度和湿度对粘虫发育历史的影响是否存在显著差异。表5-7不同温度和湿度的粘虫发育历史
7.多因素分析方差分析法使用方差分析的标准如下:
1、各种版本必须是相互不相关的随机样本;
2、各种版本来自正态分布的整体;
3、每个整体方差都是一样的,即方差齐。
方差分析的用途:
1、两个或几个样本均数之间的比较;
2、对两个或几个要素之间的交互作用进行剖析;
3、线形假设检验回归方程;
4、假设检验多元线性回归分析中偏回归系数;
5、两本书的方差齐性检验等。
由于各种条件的限制,研究室获得的数据起伏不定。变化的原因可以分为两类,一类是不可控的随机因素,另一类是增加对实验结论的可控因素。
方差分析及各种因素方差分析是衡量多个整体平均值是否相等的统计方法。它通过检测每个整体的平均值是否相同来判断分类变量是否对数值型自变量有明显的危害。
单一因素方差分析的基本概念:数据偏差即总误差平方和分组平方和同组平方和,同组偏差仅包括随机误差。组之间的偏差包括随机误差和系统偏差。系统偏差是由不同程度的元素引起的偏差。如果元素的不同程度不影响数据,系统偏差为0,通过可玩性平均值后,组之间的偏差与同组之间的偏差之间的标值对比接近1。相反,如果元素的不同程度影响数据,这个比率就会超过1。当它达到一定的意义时,可以说不同程度之间存在明显的差异。也就是变量对因变量有明显的影响。
多要素方差分析是什么?根据材料设计类型的不同,有以下两种方差分析方法:
1、对于组合定制的多个样品平均值进行比较,应采用任意定制的方差分析,即单因素方差分析。
2、对于任意区组定制的多个样品平均值进行比较,应采用搭配组定制的方差分析,即两要素方差分析。
两种方差异相同
两种方差分析的异同:
两种方差分析的基本流程是一样的,只是变异分解的方式不同。组合设计的数据总变异分解为同组变异和组变异(随机误差),即:但组合变异除分解为处理组变异和随机误差外,还包括组合变异。
十.多因素方差分析是什么?使用方差分析的标准如下:
1、各种版本必须是相互不相关的随机样本;
2、各种版本来自正态分布的整体;
3、每个方差都是一样的,也就是方差齐。方差分析的用途:
1、两个或几个样本均数之间的比较;
2、对两个或几个要素之间的交互作用进行剖析;
3、线形假设检验回归方程;
4、假设检验多元线性回归分析中偏回归系数;
5、两本书的方差齐性测试等。由于各种条件的限制,研究室获得的数据呈波动状。变化的原因可以分为两类,一类是不可控的随机因素,另一类是增加影响结论的可控因素。
方差分析多因素分析怎么操作?方差分析过程:
①创造原始假设和备泽假设,原始假设是:不同水平对应相同的平均值;
②给出明显的标准α,默认0.05;
③F0值(F0=偏差可玩性/模型可玩性)计算F统计量。
假设方差条件为残差服从正态分布,其标准等于:
①每组观察服从正态分布(如果观察量足够,则认为正态分布);
②方差齐性;
③在数据中,观察间是分开的。
三个过程步骤适用于方差分析:TTEST、ANOVA、每个GLM都适用一个元素2个标准。(TTEST\ANOVA\GLM)、多个层次的元素(ANOVA\GLM)、多个要素(ANOVA\GLM)。不同的是ANOVA适用于解决平衡数据(每个分类观察总数相同)。
相关文章

有许多的朋友最近问小编佛手柑精油的功效与作用与操作方法(佛手柑精油的功效与作用)的问题,那么小编收集整合后,今天为大家分享关于的相关文章,一起来了解一下吧!1.佛手柑精油的功效与作用与操作方法柠檬精油护肤作用:柠檬
2024-08-31 15:24:01
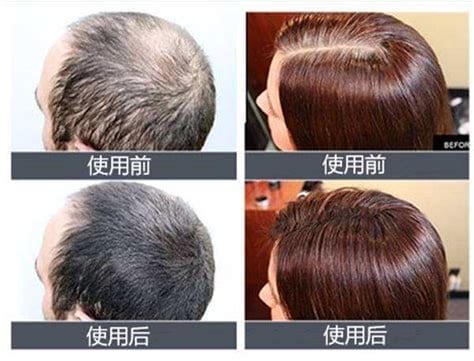
生活中,很多小伙伴不知道增发纤维副作用(增发纤维的危害性),今天小编针对这个问题做了这篇文章,详细内容我们来看一下。增发纤维的危害归根结底,头发纤维粉是一种物理密发产品,纤维粉通过纳米切割技术由天然草棉纤维匀称切
2024-08-31 15:12:02

生活中,很多小伙伴不知道薏湿糕的功效与作用禁忌,今天小编针对这个问题做了这篇文章,详细内容我们来看一下。薏湿糕是如今比较火的一款保健品,蛮多人当零食吃的,想知道薏湿糕的功效与作用忌讳有什么?它的主要成分有薏苡仁、
2024-08-31 15:00:01

生活中有些小伙伴会遇到根豆粉有哪些作用(根豆粉的功效和秘方使用量是什么?)的问题,没有关系,通过这篇文章就能帮大家轻松解决,跟着小编我们一起来看下正文。根豆粉的作用和秘方用量是啥?开胃消暑多吃“蕨根粉”在炎热的
2024-08-31 13:00:01

在生活的过程中我们经常会遇到许多的问题,就有朋友问小编有关的问题,那么今天小编就和大家来聊一聊,一起来看看吧。菜是一种常见的蔬菜,野外见的是很多的,别看它随处可见,可是作用却很多呢,并且在使用的时候多多注意忌讳也是
2024-08-31 12:24:01